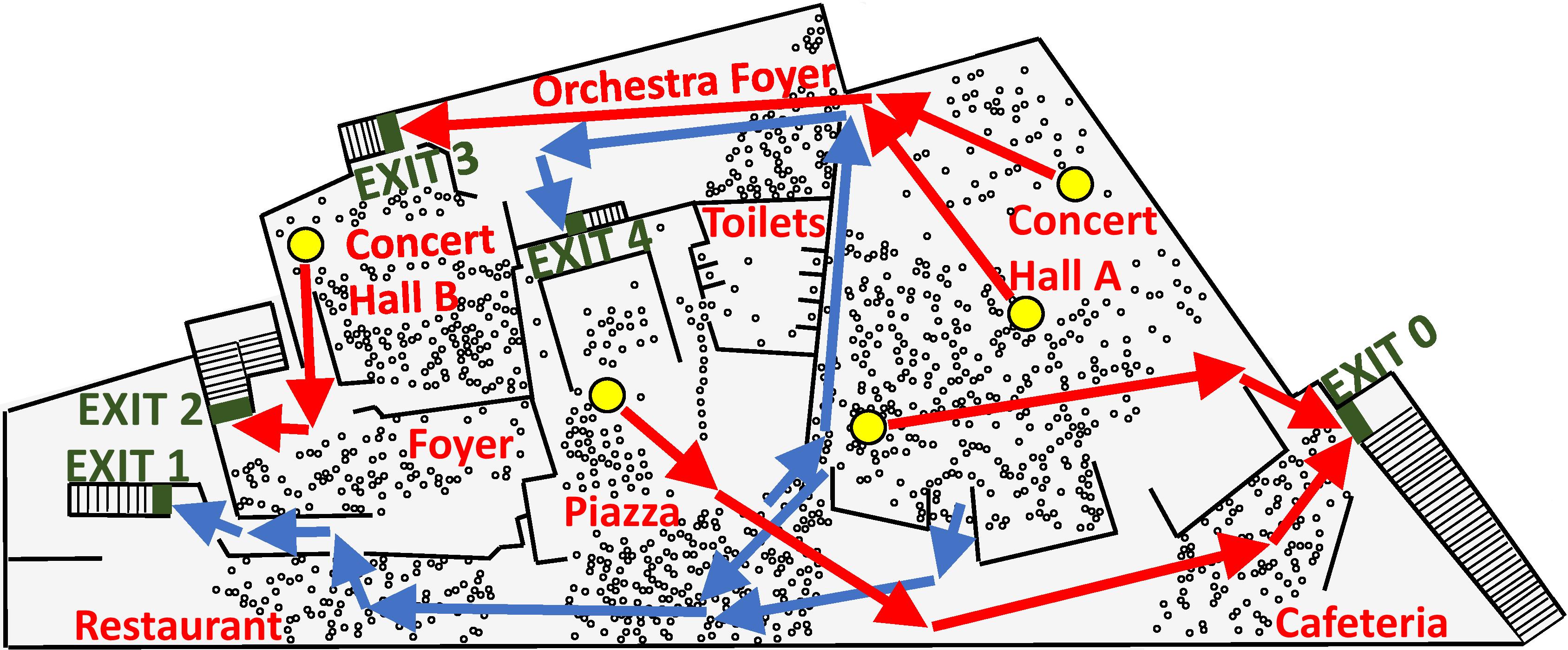
Our crowd dynamics and evacuation research started in 2005 when Harri Ehtamo, Simo Heliövaara, Simo Hostikka, and Timo Korhonen started collaboration between the Department of Mathematics and Systems Analysis at Aalto University and the Fire Safety Research group at VTT Technical Research Centre of Finland. Together with VTT, we have been developing the widely-used fire and crowd dynamics simulator FDS, and an evacuation simulation module Evac of it (Korhonen and Hostikka, Technical Report VTT, 2009). FDS+Evac has been used, e.g., in the fire safety design of Helsinki Music Centre. The research collaboration has also resulted in three Ph.D. theses during the years 2005-2021.
One of the highlights was the doctoral dissertation by Anton von Schantz that took place in Aalto-University in June 2021, with a related one page science news article in the newspaper Helsingin Sanomat (Helsingin Sanomat/Tiede, 24.6.2021, p. 79).
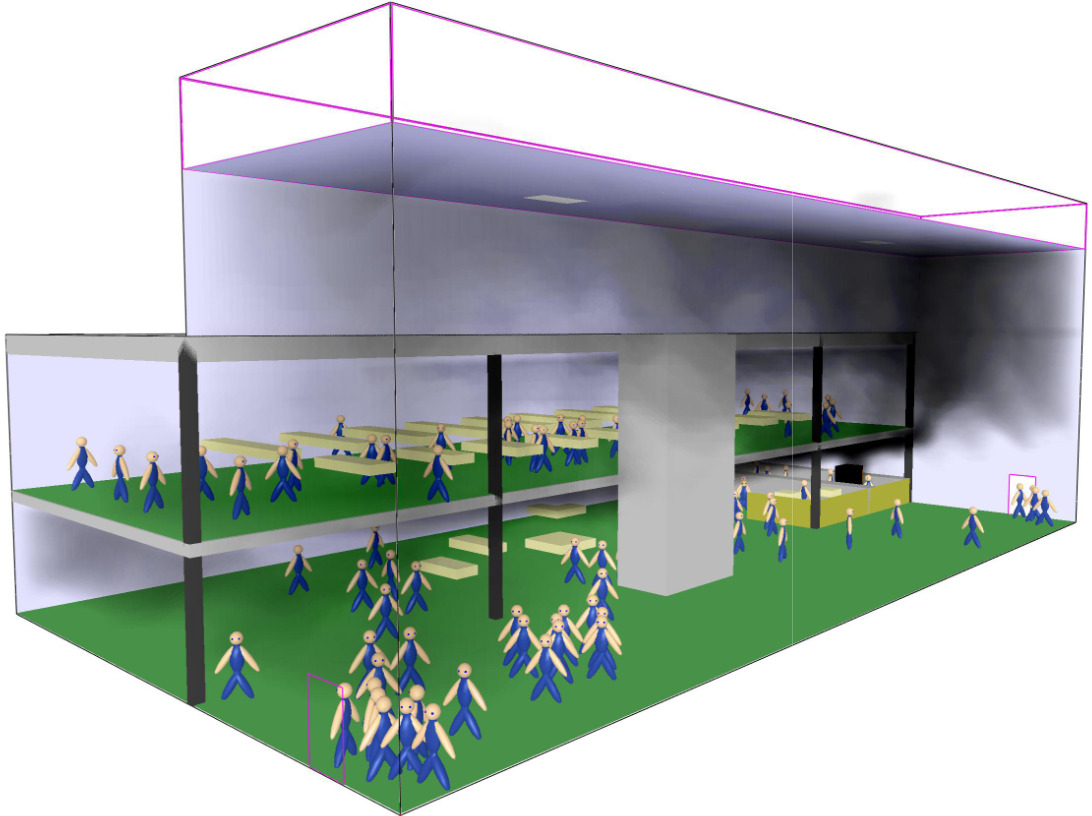
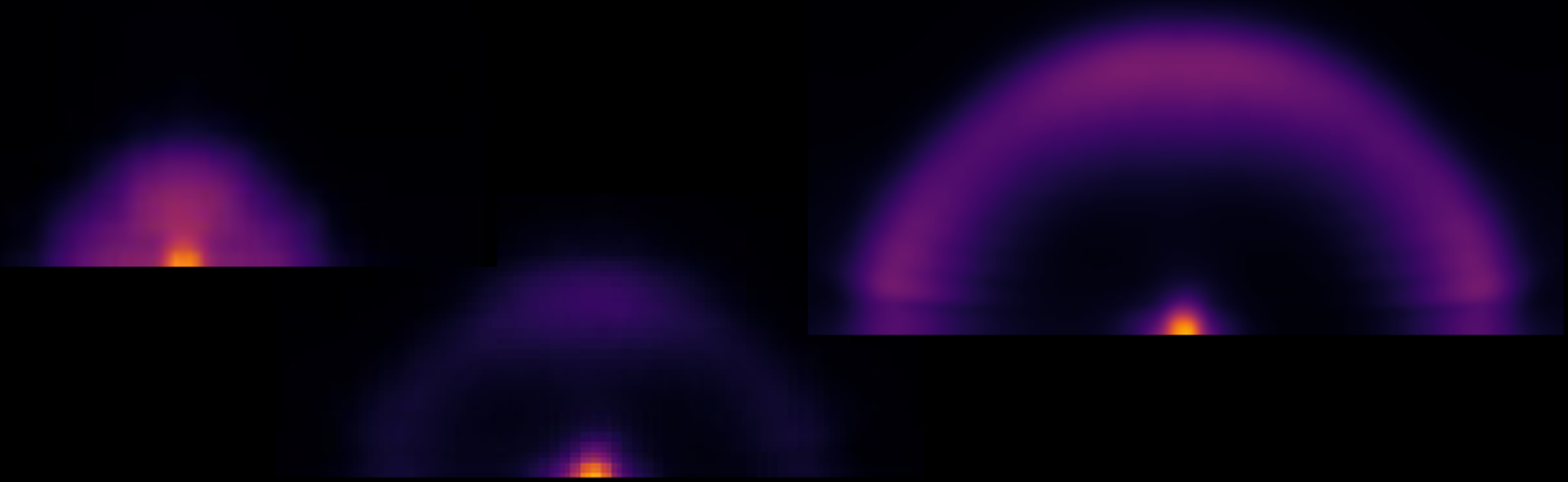







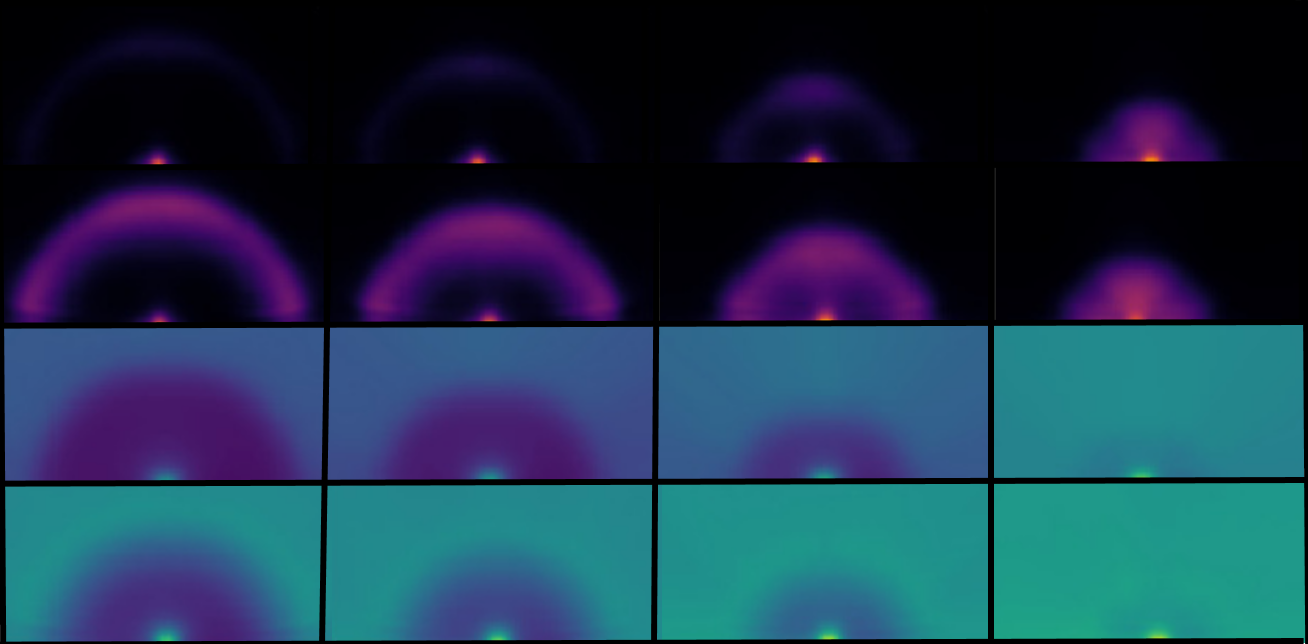
 Large mass gatherings and crowded festivals may cause crowd congestions. Sometimes, the threat to the crowd members is the escaping crowd itself that may originate panic. If there are too many pedestrians in a scarce or dwindling space, a stampede or escape panic may occur. According to empirical investigations: (1) People move or tend to move considerably faster than normal. (2) Individuals start pushing, and interactions among people become physical in nature. (3) Moving and, in particular, passing of a bottleneck becomes uncoordinated. (4) At exits, arching and clogging are observed. (5) Jams build up. (6) The physical interactions in the jammed crowds add up and cause dangerous pressures, which can push down brick walls (Helbing et al., Nature, 2000).
Large mass gatherings and crowded festivals may cause crowd congestions. Sometimes, the threat to the crowd members is the escaping crowd itself that may originate panic. If there are too many pedestrians in a scarce or dwindling space, a stampede or escape panic may occur. According to empirical investigations: (1) People move or tend to move considerably faster than normal. (2) Individuals start pushing, and interactions among people become physical in nature. (3) Moving and, in particular, passing of a bottleneck becomes uncoordinated. (4) At exits, arching and clogging are observed. (5) Jams build up. (6) The physical interactions in the jammed crowds add up and cause dangerous pressures, which can push down brick walls (Helbing et al., Nature, 2000).


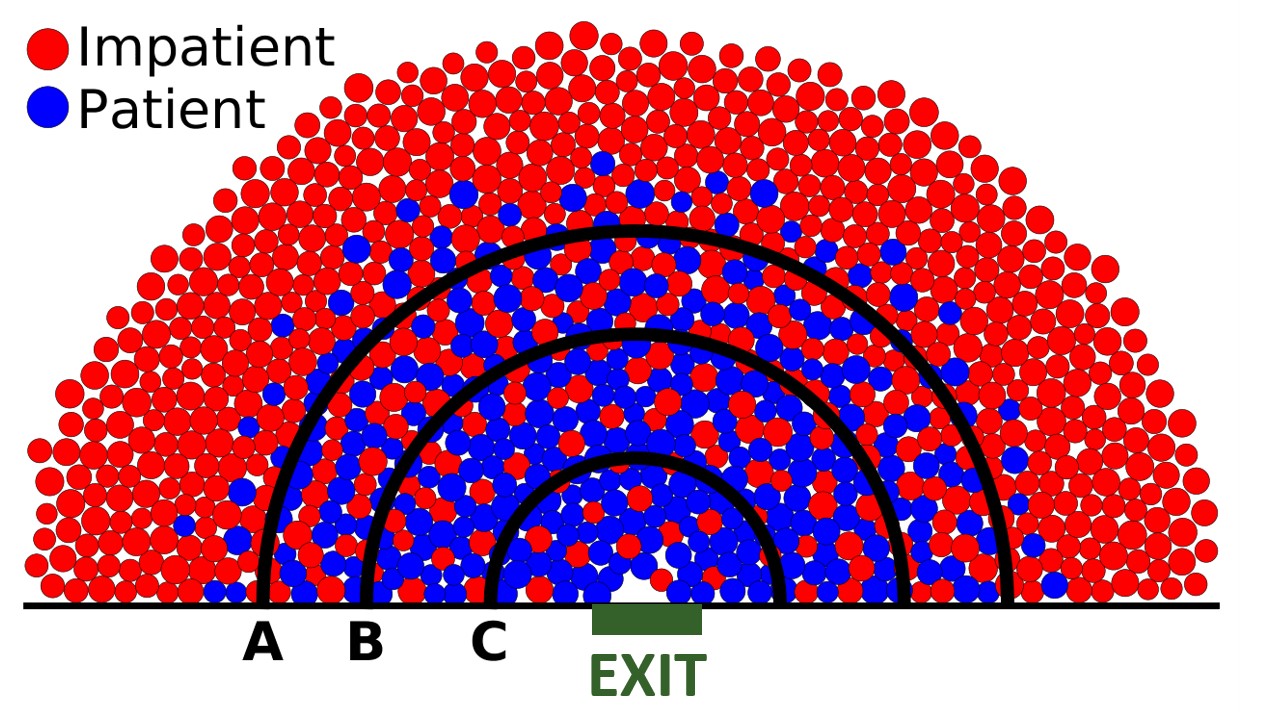 For a competitive exit congestion, we develop an evolutionary game, where the agents play against their nearest neighbors. The agents have two strategies to choose from: Patient and Impatient. It is assumed that these strategies correspond to their patient and impatient behaviors in an actual play of the game. In a numerical congestion simulation, the proportion of impatient agents increases with the distance to the exit. This is natural since here time is a limited resource.
For a competitive exit congestion, we develop an evolutionary game, where the agents play against their nearest neighbors. The agents have two strategies to choose from: Patient and Impatient. It is assumed that these strategies correspond to their patient and impatient behaviors in an actual play of the game. In a numerical congestion simulation, the proportion of impatient agents increases with the distance to the exit. This is natural since here time is a limited resource.